Linked lists are one of the topics that are discussed broadly in interviews. If you have gone to any kind of higher-level technical interview, then you might have definitely been asked about Linked Lists and you might have ended up with a problem statement where you have to use Linked Lists.
In this blog I will be discussing one of the problem statements that you can solve using a Linked List which is polynomial multiplication.
I will divide this whole solution into small parts so that we can go through from the very basic understanding of the approach till the end solution.
So, make sure that you read till the end to get the whole code and also understand all the bits and pieces of that code.
What Will You Learn?
Representing The Polynomial With Linked List Node
Let us first understand how we will represent the polynomial expression using a Linked List.
Polynomial is made-up of terms and each term contains a coefficient and a power. In a Linked List, every node will represent this single term.
The list node will contain a coefficient and a degree.
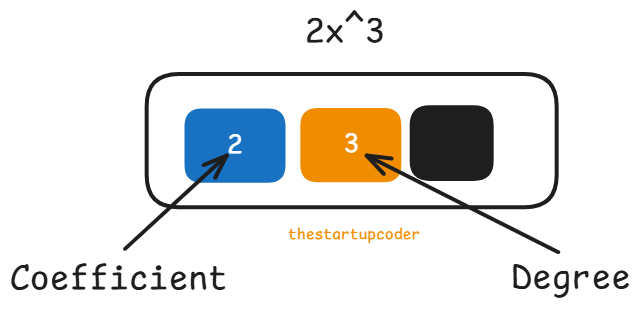
In this diagram you can see, the term 2^3 is expressed as a node with a coefficient value of two and a degree value of three.
To express the whole polynomial using a Linked List, what we can do is every previous term can point to the next term using a pointer.
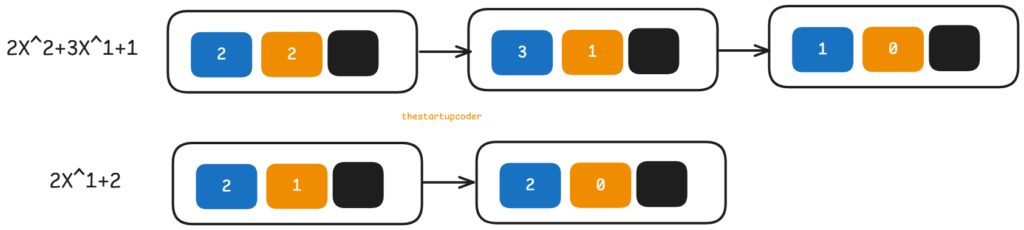
In this diagram, as you can see, I have represented 2X^2+3X+1 and 2X+1 with Linkedlist.
Structure of Each Polynomial Term In C
typedef struct Term
{
int coefficient;
int degree;
struct Term *next_node;
} Term;Term class represents each term as a Linked List node. The class contains three public variables. One is the coefficient which is an int, another one is degree which is also an int. Along with it, I have a pointer which has a type of Term, which means it is created to point to other similar Term types.
Creating and Printing Polynomial Expression
This is a simpler part where you are just creating the Linked List which is very much important before you do any kind of multiplication in the polynomial expressions. Also, we are printing the polynomial expression.
This part is fairly simple, and I just want to cover it as soon as possible so that we can jump into the main section.
This section simply covers all the basics of Linked List – creating a node, inserting a node, and printing the Linked List.
Code here is pretty much the same, but with some changes related to the `Node` structure and how we are printing the polynomial.
Term *createTerm(int coefficient, int degree)
{
Term *new_node = (Term *)malloc(sizeof(Term));
new_node->degree = degree;
new_node->coefficient = coefficient;
new_node->next_node = NULL;
return new_node;
}
Term *insertTerm(Term *head, int coefficient, int degree)
{
Term *new_node = createTerm(coefficient, degree);
if (head == NULL)
{
head = new_node;
}
else
{
Term *current = head;
while (current->next_node != NULL)
{
current = current->next_node;
}
current->next_node = new_node;
}
return head;
}
void printPolynomial(Term *head)
{
Term *current = head;
while (current != NULL)
{
printf("%dx^%d", current->coefficient, current->degree);
if (current->next_node != NULL)
{
printf(" + ");
}
current = current->next_node;
}
printf("\n");
}
You can see that I am using the coefficient*X^degree. And then not giving any new line, I’m just adding a plus sign and going to the next term. I will not add + if that is the last node.
Multiplying Two Polynomials
First, let’s understand the basics of how you would multiply 2 polynomials mathematically outside of programming.
Out of the two polynomials, you will first take the shortest polynomial, and you will take one of the leftmost terms from it. Then you will choose the other polynomial and multiply each term of that other polynomial from left to right with the term that you have chosen from the shortest polynomial.
You will follow this same technique for the other terms of the shorter polynomial and finally after you are done with multiplying all the terms, you will get a very long polynomial expression where you will see some of the terms have the same degree.
Finally, you will just add those terms that have the same degree and get your final result.
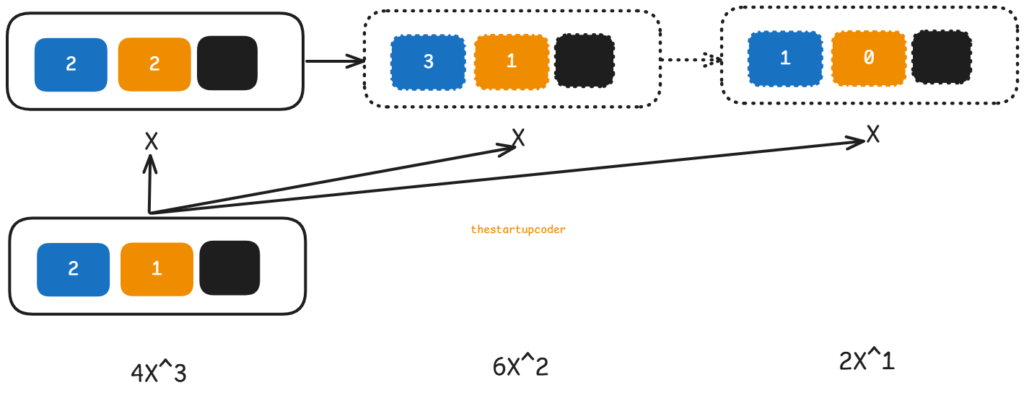
This solution also focuses on the same technique.
Inside a loop, first in every iteration I will take one term from one of the polynomials. Then in an inner loop, I will go through the terms of the other polynomial and multiply my current term with.
When multiplying, I will multiply the coefficients, and I will add the degrees. After I get the coefficient and the degree of the current term, I will save it inside a map where the key will be the degree, and the coefficient will be added to the previous value.
So, after multiplying, if we see a term with a power of 3 and coefficient 2, then after some further multiplication we again see another term which has power of 3 with coefficient 1. Using this mapping we will get the total coefficient value for the degree 3 as 3. Which is correct!
Lastly, we will just convert this mapping into a resultant Linked List.
Term *multiplyPolynomial(Term *p1_head, Term *p2_head)
{
Term *p1 = p1_head;
map *dc_map = (map *)malloc(sizeof(map) * MAX);
init_map(dc_map, MAX);
int max_degree = 0;
while (p1 != NULL)
{
Term *p2 = p2_head;
while (p2 != NULL)
{
int degree = p1->degree + p2->degree;
int coefficient = p1->coefficient * p2->coefficient;
max_degree = degree > max_degree ? degree : max_degree;
map m = getValue(dc_map, degree);
if (m.value == 0)
{
setValue(dc_map, degree, coefficient);
}
else
{
setValue(dc_map, degree, m.value + coefficient);
}
p2 = p2->next_node;
}
p1 = p1->next_node;
}
Term *result = NULL;
for (int d = 0; d <= max_degree; d++)
{
map m = getValue(dc_map, d);
if (m.value != 0)
{
printf("%d %d\n", m.key, m.value);
}
}
for (int d = max_degree; d >= 0; d--)
{
map m = getValue(dc_map, d);
if (m.value != 0)
{
result = insertTerm(result, m.value, m.key);
}
}
return result;
}
Code For Polynomial Multiplication
This is the final code of this whole implementation.
#include <stdio.h>
#include <stdlib.h>
#define MAX 100 // Maximum degree of polynomial
typedef struct map
{
int key;
int value;
} map;
void init_map(map *dc_map, int size)
{
for (int i = 0; i < size; i++)
{
dc_map[i].key = i;
dc_map[i].value = 0;
}
}
map getValue(map *dc_map, int degree)
{
if (degree < 0)
{
map m = {-1, -1};
return m;
}
return dc_map[degree];
}
void setValue(map *dc_map, int degree, int value)
{
dc_map[degree].key = degree;
dc_map[degree].value = value;
}
typedef struct Term
{
int coefficient;
int degree;
struct Term *next_node;
} Term;
Term *createTerm(int coefficient, int degree)
{
Term *new_node = (Term *)malloc(sizeof(Term));
new_node->degree = degree;
new_node->coefficient = coefficient;
new_node->next_node = NULL;
return new_node;
}
Term *insertTerm(Term *head, int coefficient, int degree)
{
Term *new_node = createTerm(coefficient, degree);
if (head == NULL)
{
head = new_node;
}
else
{
Term *current = head;
while (current->next_node != NULL)
{
current = current->next_node;
}
current->next_node = new_node;
}
return head;
}
void printPolynomial(Term *head)
{
Term *current = head;
while (current != NULL)
{
printf("%dx^%d", current->coefficient, current->degree);
if (current->next_node != NULL)
{
printf(" + ");
}
current = current->next_node;
}
printf("\n");
}
Term *multiplyPolynomial(Term *p1_head, Term *p2_head)
{
Term *p1 = p1_head;
map *dc_map = (map *)malloc(sizeof(map) * MAX);
init_map(dc_map, MAX);
int max_degree = 0;
while (p1 != NULL)
{
Term *p2 = p2_head;
while (p2 != NULL)
{
int degree = p1->degree + p2->degree;
int coefficient = p1->coefficient * p2->coefficient;
max_degree = degree > max_degree ? degree : max_degree;
map m = getValue(dc_map, degree);
if (m.value == 0)
{
setValue(dc_map, degree, coefficient);
}
else
{
setValue(dc_map, degree, m.value + coefficient);
}
p2 = p2->next_node;
}
p1 = p1->next_node;
}
Term *result = NULL;
for (int d = 0; d <= max_degree; d++)
{
map m = getValue(dc_map, d);
if (m.value != 0)
{
printf("%d %d\n", m.key, m.value);
}
}
for (int d = max_degree; d >= 0; d--)
{
map m = getValue(dc_map, d);
if (m.value != 0)
{
result = insertTerm(result, m.value, m.key);
}
}
return result;
}
int main()
{
Term *p1_head = NULL;
p1_head = insertTerm(p1_head, 3, 2);
p1_head = insertTerm(p1_head, 2, 1);
p1_head = insertTerm(p1_head, 1, 0);
printPolynomial(p1_head); // 3x^2 + 2x^1 + 1
Term *p2_head = NULL;
p2_head = insertTerm(p2_head, 2, 1);
p2_head = insertTerm(p2_head, 1, 0);
printPolynomial(p2_head); // 2x^1 + 1
Term *result = multiplyPolynomial(p1_head, p2_head);
printPolynomial(result); // 6x^3 + 7x^2 + 4x^1 + 1
return 0;
}Conclusion
Linked list could be easy if you practice it a lot, but it could be very difficult to understand if you do not practice with different kinds of problems.
So, it is important that you make sure you go through this problem again. If you do not understand it properly, try to implement it by yourself. Look at the output and see whether you can make sense out of it.
Also encourage you to go through other similar problems using Linked List so that you can Polish your knowledge in Linked List, and you can be confident in answering any kind of link list related questions at interviews if asked.
Liked this blog? Start reading this blog from The Startup Coder.
References:

