What Is Memorization In dynamic Programming?

Memorization is one of the techniques used in dynamic programming. It is an optimization technique, that you can use to reduce the time complexity of any algorithm. But, what is memorization in dynamic programming?

Memorization can be difficult to understand without an example. If you are someone who is struggling to understand memorization in dynamic programming,

And want to understand it using a simple example, then you have come to the right place!

We are going to dive deep into memorization through an example in this blog.

You have already seen this example many times in your programming journey.

Memorization enhances the performance of algorithms by reusing and storing expensive function calls. Memorization is a Latin word that comes from “memorandum” where “memo” means “to remember”.

Let’s look at the example that will help you understand memorization better.

Fibonacci Series

Fibonacci series is a famous problem that you always see in your programming journey a lot of times. No matter which programming language, you might have solved it.

You don’t know what is fibonacci series?

Then let’s first understand the general concept of fibonacci series.

It is a series, and the logic of the series is,

If you want to get the n’th Fibonacci number then you have to add (n-1)th fibonacci number with (n-2)th fibonacci number.

For example, 3rd fibonacci number will be – fib(3)=fib(2)+fib(1)

In this series, fib(0) = 0, and fib(1) = 1. You can use these initial values to compute any n’th fibonacci value.

You usually will use recursion to solve Fibonacci series and you will write code like the following –

int fib(int n)
{
    if (n == 0 || n == 1)
    {
        return n;
    }
    return fib(n - 1) + fib(n - 2);
}

But what’s the problem with solving Fibonacci series with recursion? And why do we need memorization to solve this problem? Let’s discuss that next.

What Is Memorization In Dynamic Programming

Let’s understand why we need memorization for Fibonacci series.

We need to first draw the recursion tree for the recursion logic written in the code.

If you closely look at the diagram,

Then you will see that fib(3) appears 2 times. fib(2) appears 3 times. In fib(5) only, you can see that there are lots of overlapping problems. As you increase n, the number of overlapping problems will increase.

That is where we need memorization. And we can reduce a lot of time complexity by doing so.

With recursion, you will have an exponential time complexity, which is huge.

But if you do the same using memorization then it will take linear time. Can you see the improvement we get by using memorization?

Now, you might have a question now…

How do I solve this problem using memorization? 

Let’s try to understand that.

Solving Fibonacci Using Memorization

In Fibonacci series, we first store the computations in an array,

Then reuse these values when the same computations occur in the future.

In this way, we make sure that we do not recompute the same value.

In the example it means,

We will save the value of fib(3) and fib(2) and then we will reuse this same value when we see it the next time.

How the code will look like if you try to solve this Fibonacci series using memorization?

This is how the code will look like.

int memo[] = {-1, -1, ..., -1};

int fib(int n)
{
    int res;
    if (memo[n] == -1)
    {
        if (n == 0 || n == 1)
        {
            res = n;
        }
        else
        {
            res = fib(n - 1) + fib(n - 2);
        }
        memo[n] = res;
    }
    return memo[n];
}

As you can see, the solution is very close to the recursion solution.

The only difference here is,

We are using an array called memo, which stores the values that are already computed,

And if later we see the same computation, then we can return the value stored in this memo array.

The logic is that we are always checking whether the memo value at n is -1 or not,

If it is -1 then fib(n) is not yet calculated and we have to do recursion to find the result. But if we see that the memo value is not -1,

Then it means that fib(n) is already calculated and we can reuse the value from memo array.

Next, I will show you how the memorization solution will look like for fib(5) to make the concept clear.

Memorization Example

I will take the example of fib(5) and try to calculate fib(5) using memorization.

As you might have seen in the previous code we are first initializing the whole memo array -1. Now this initial value could vary depending on the problem that you are trying to solve.

You just have to initialize the memo array with a value that is not possible to appear. For fibonacci, -1 is a value that will never come. That’s why I am using -1 to check whether the value is already calculated or not. You can use any other negative value as well.

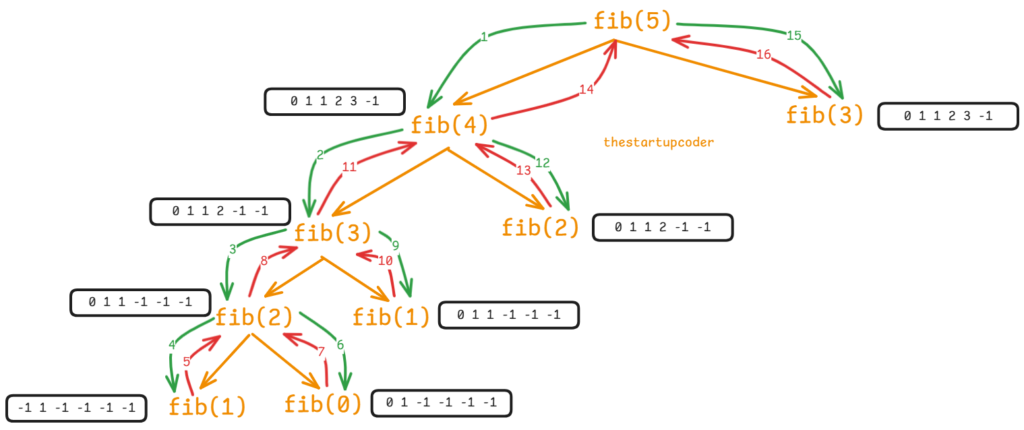
We start the recursion tree from fib(5). 1st we check whether the memo value at 5 is -1 or not. We see that it is -1, so we do the recursion and call fib(4).

In fib(4), we again see that memo value at 4 is -1. So we recursively solve for fib(3).

In fib(3) the same thing happens. We try to derive the value for fib(2) and then from fib(2) we go to fib(1).

In fib(1), we see the memo value is -1, We go inside the if block and return 1. We also save the memo[1]=1 before returning.

We go back to the parent function which is fib(2). Then fib(2) calls fib(0).

fib(0) returns 0. We also save memo[0]=0.

So till now the values that we have calculated are for fib(0) and fib(1). And memo = [0, 1, -1, -1, -1, -1] (the size of the array is n+1).

We also store the value for fib(2) in the memo before returning to its parent function fib(3). memo=[0, 1, 1, -1, -1, -1]

In fib(3), it will try to call fib(2). And here comes the memorization magic. 

fib(2) value is already calculated,

memo[2] is not -1, so instead of calculating it again, we will just return the value from the memo[2] which is 1. Before returning, we save the fib(3) in memo. memo=[0, 1, 1, 2, -1, -1].

Now memo array also contains the calculation for fib 3.

If you follow the same logic, you will see that when we go back to fib(5) again, we already have memo array [0, 1, 1, 2, 3, -1]. 

fib(5) will try to call its right child which is fib(3), but it is already calculated. And it will return the memo[3]=2.

You can see in this way we are saving a lot of recomputations.

If you take a look at the recursion tree,

You will see that the number of times fib(5) computes and calls functions are not more than 2. So from fib(0) to fib(5), every function will take memory at most 2 times,

Which makes the time complexity of this solution linear. 

Another good example of memorization in dynamic programming –

Conclusion

Now that you have seen how memorization can improve your algorithms,

You must practice some more examples using memorization to solidify the concept.

If you see any problem that is solved using recursion,

And there are overlapping subproblems – You can be sure to use memorization.

Coming up with memorization is easy, as long as you know the recursive solution.

Want to dive more into DSA? Then read my next blog about stack and queue implementation with C.